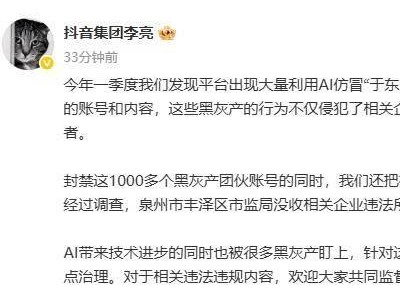
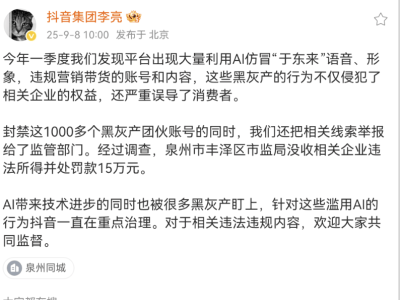
科技领域近日掀起一场关于大语言模型(LLM)能力边界的讨论,起因源于一项对比实验:当被要求判断超大偶数是否为质数时,不同模型展现出截然不同的解题逻辑。这场由开发者路易斯发起的测试,经埃隆·马斯克转发后迅速引发热议,核心焦点集中在模型对数学常识的掌握与工具调用策略的差异上。
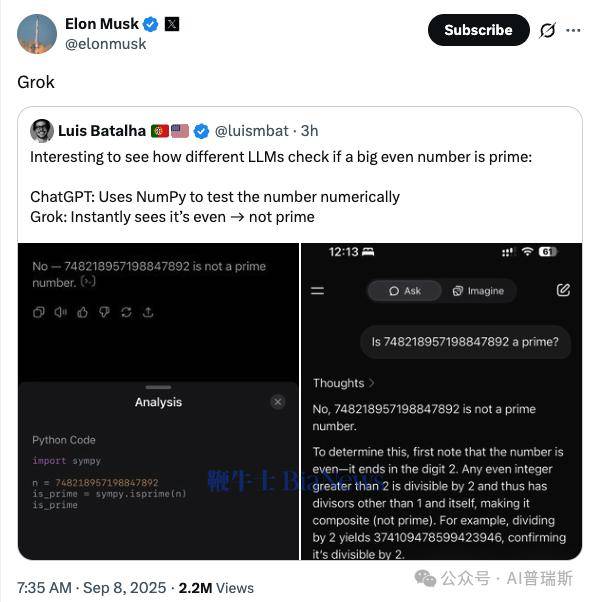
实验中,测试者向多个大模型抛出同一问题:"748218957198847892是否为质数"。这一数字的特殊性在于,它既是超过百位的超大整数,又明显符合偶数的数学特征。面对此类问题,不同模型给出了迥异的解决方案。
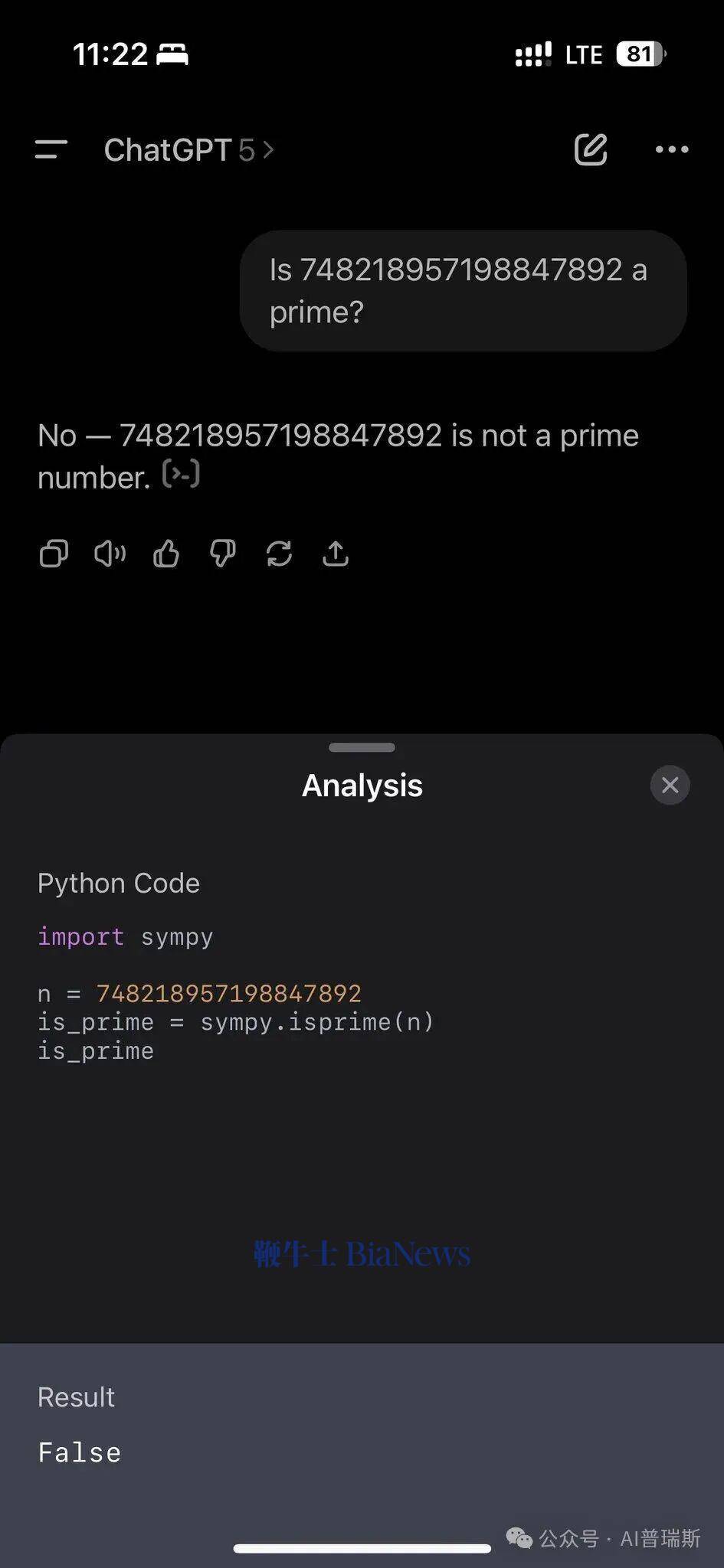
ChatGPT的应对策略体现了典型的工程思维。该模型首先调用NumPy数值计算库,试图通过穷举法验证该数是否存在除1和自身外的因数。尽管这种"暴力计算"在理论上可行,但对于百位级数字而言,实际运算量远超常规计算范围,导致系统长时间无响应。这种依赖外部工具的路径选择,折射出模型对数值验证的严谨态度。
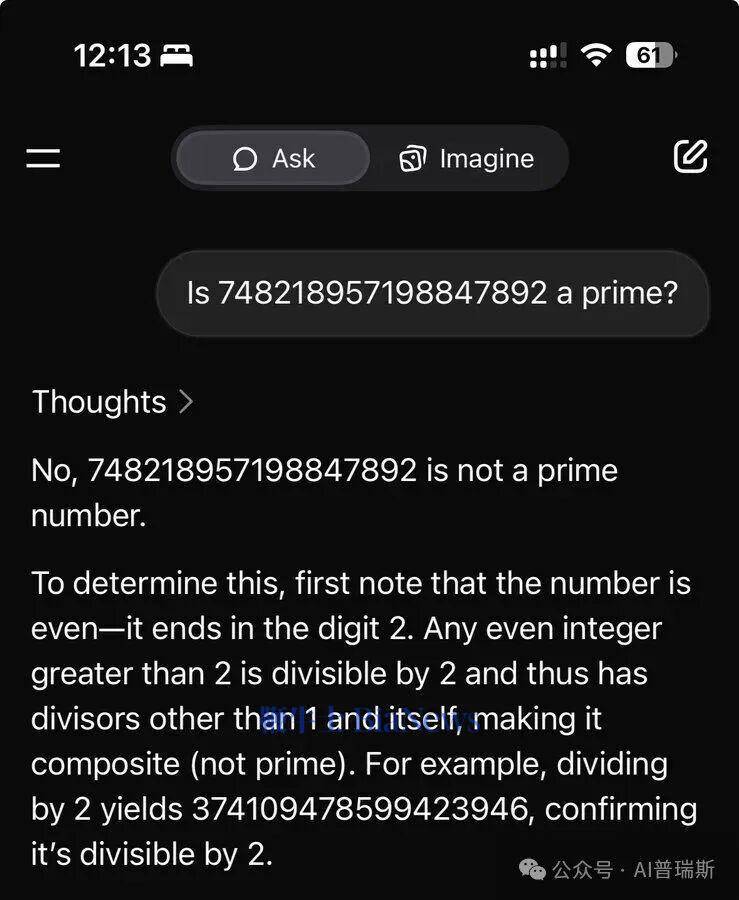
与之形成鲜明对比的是X平台旗下Grok的表现。该模型未启动任何计算工具,而是直接应用"所有大于2的偶数均非质数"这一基础数学定理,在毫秒级时间内给出否定答案。这种"直觉式"的解题方式,展现了模型对数学常识的深度内化,以及将抽象理论快速映射到具体问题的能力。
两种路径的碰撞引发行业深度思考。有专家指出,ChatGPT的方案虽显笨拙,却体现了模型与外部系统协同的潜力,这种"工具增强型智能"在需要精确数值的场景中具有优势。而Grok的表现则证明,当模型能准确识别问题本质时,常识储备可转化为高效的决策能力。如何平衡这两种能力,成为当前模型优化的关键课题。
测试结果还揭示出大模型发展中的深层矛盾:过度依赖工具可能导致基础能力退化,而片面强调常识储备又可能限制复杂问题的解决。这场看似简单的数学测试,实则叩响了人工智能发展路径选择的大门——是追求"全能计算器",还是培育"逻辑推理者",或许需要重新审视模型设计的底层逻辑。